Activation Functions: Why Neural Networks Need Them

Last week, we covered forward and backward propagation - how neural networks make predictions and learn from their mistakes.

This week, let's talk about activation functions.

You've probably heard: "Neural networks need activation functions" or "They must be non-linear."

But why? What problem do they actually solve?

Let's break it down.

Why We Need Activation Functions

Imagine you build a neural network without any activation functions.

Just neurons doing multiplication and addition. Stack multiple layers. Connect them together.

Seems reasonable, right?

Here's the problem: it doesn't work.

Linear vs Non-Linear Functions

To understand why, we need to understand what "linear" and "non-linear" mean.

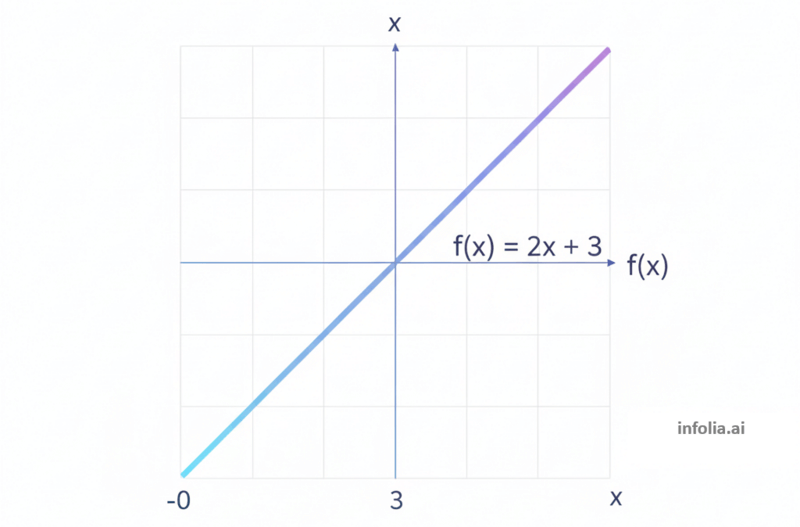
Linear Functions

A linear function is just multiplication and addition.

f(x) = 2x + 3

That's linear. Multiply by 2, add 3.

If you graph it, you get a straight line.

Double the input? The output changes in a predictable way. Always a straight line.

Non-Linear Functions

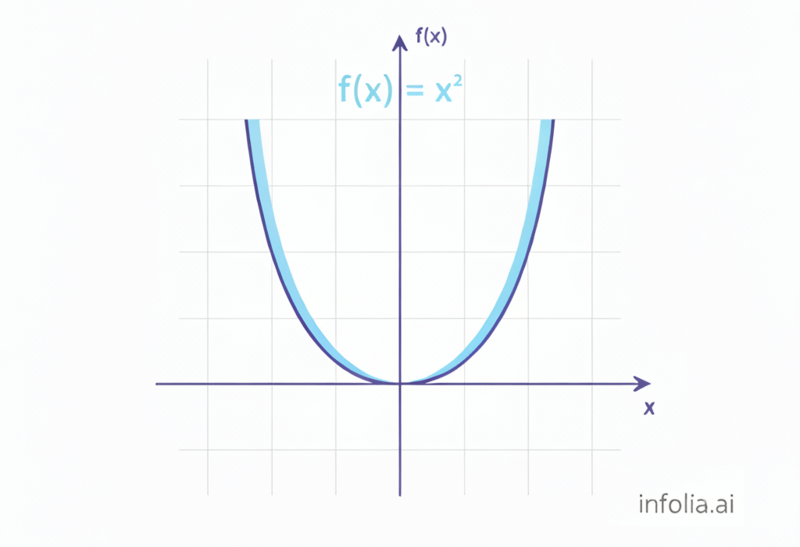
A non-linear function creates curves and bends.

f(x) = x²

This is non-linear. Graph it, you get a curve (a parabola).

The output doesn't change proportionally. Sometimes it goes up slowly, sometimes quickly. It curves.

The Stacking Problem

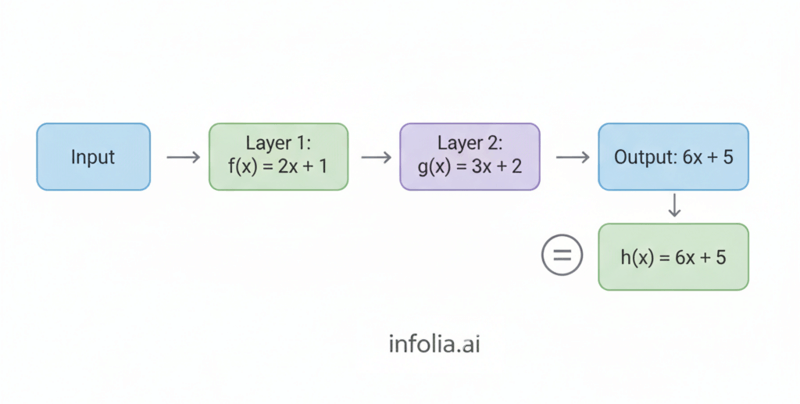
Here's what happens when you stack linear functions.

Say you have two layers:

Layer 1: f(x) = 2x + 1
Layer 2: g(x) = 3x + 2

When you connect them (output of layer 1 goes into layer 2):

g(f(x)) = g(2x + 1)
        = 3(2x + 1) + 2
        = 6x + 3 + 2
        = 6x + 5

Look at the result: 6x + 5

Still just multiplication and addition. Still linear.

You could have 10 layers, 100 layers, 1000 layers. Doesn't matter.

Mathematically, it all collapses into one equation: mx + b

All that depth? All those layers? Useless.

Your "deep" neural network is mathematically identical to a single-layer network.

Real-World Problems Need Non-Linearity

This is a problem because real-world data isn't linear.

Example 1: Image Classification

You're building a cat vs dog classifier.

The difference between "cat" and "dog" in pixel space isn't a straight line.

It's complex. It's curved.

A straight line can't separate cats from dogs. You need curves and complex shapes.

Example 2: Language Understanding

Consider: "This movie is not bad"

A linear model sees "not" and "bad" → thinks negative.

But the actual meaning is positive (double negative).

Understanding this requires non-linear processing.

Example: XOR Problem

You have four points:

• (0,0) → Class A
• (0,1) → Class B
• (1,0) → Class B
• (1,1) → Class A

Try drawing a single straight line that separates Class A from Class B.

You can't. No straight line works.

You need a curved boundary. You need non-linearity.

Input (x,y)	Class	Linear Separable?
(0,0)	Blue	No - needs
(0,1)	Red	curved boundary
(1,0)	Red
(1,1)	Blue

How Activation Functions Fix This

Activation functions introduce non-linearity into the network.

They break the "stacking linear = still linear" problem.

Without Activation Functions

Input → [Linear] → [Linear] → [Linear] → Output

Result: Everything collapses to mx + b

With Activation Functions

Input → [Linear] → [Activation] → [Linear] → [Activation] → Output

Result: Complex non-linear transformation

The activation function bends the mathematical space. Allows the network to create curves, not just straight lines.

Without them, depth is meaningless. With them, each layer can learn something new.

WITHOUT ACTIVATION FUNCTIONS:
Input → [Layer 1] → [Layer 2] → [Layer 3] → Output
\t\u2193
Collapses to:
Input → [Single Linear Function] → Output

WITH ACTIVATION FUNCTIONS:
Input → [Layer 1] → [ReLU] → [Layer 2] → [ReLU] → [Layer 3] → Output
(Each layer learns something new)

The Three Main Activation Functions

Now let's look at the three most common activation functions.

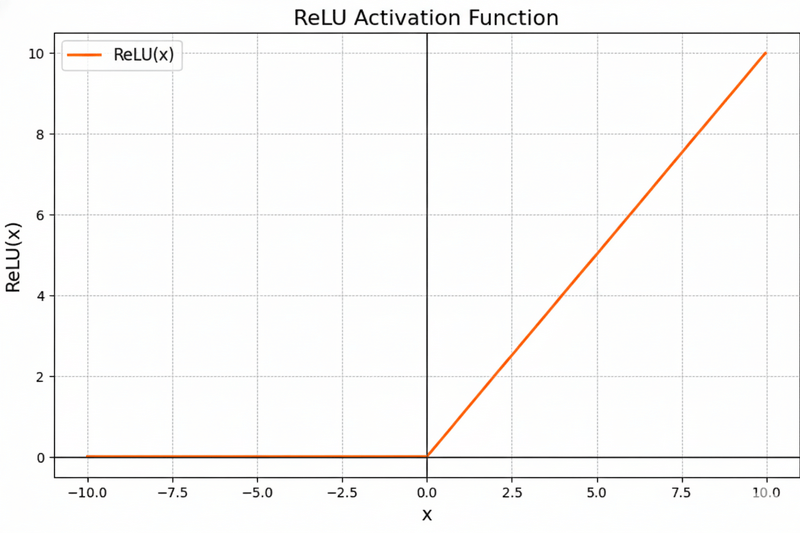
1. ReLU (Rectified Linear Unit)

The simplest one.

ReLU(x) = max(0, x)

What it does:

• If x is positive → keep it
• If x is negative → make it zero

Example:

ReLU(5) = 5
ReLU(-3) = 0
ReLU(0.7) = 0.7
ReLU(-0.2) = 0

If you graph it: diagonal line for positives, flat at zero for negatives.

That bend at zero makes it non-linear.

When to use it:

Default choice for hidden layers. 90% of the time, use ReLU.

Why?

• Fast to compute (just check if x > 0)
• Works well in deep networks
• Simple but effective

The problem:

Sometimes neurons "die" - get stuck at zero and never recover. Called the "dying ReLU" problem.

In practice, not a huge issue.

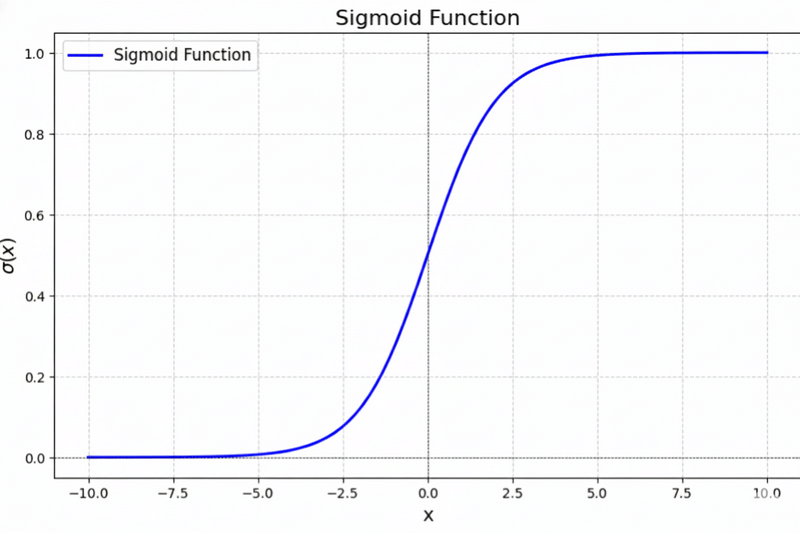
2. Sigmoid

Squashes everything between 0 and 1.

Sigmoid(x) = 1 / (1 + e^(-x))

What it does:

• Large positive input → close to 1
• Large negative input → close to 0
• Around zero → around 0.5

Creates a smooth S-shaped curve.

Example:

Sigmoid(5) \u2248 0.99
Sigmoid(0) = 0.5
Sigmoid(-5) \u2248 0.01

When to use it:

Mainly for output layers when you need probabilities.

Example: "Is this a cat?"

• Output 0.9 → 90% confident it's a cat
• Output 0.1 → 10% confident (probably not)

The problem:

"Vanishing gradient" - in deep networks, gradients become tiny. Learning becomes slow.

That's why we don't use sigmoid in hidden layers anymore. ReLU is better.

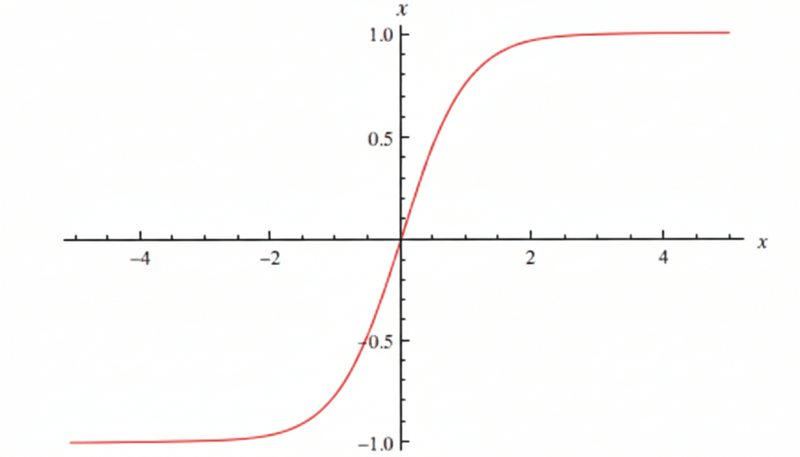
3. Tanh (Hyperbolic Tangent)

Similar to sigmoid, but outputs between -1 and 1.

Tanh(x) = (e^x - e^(-x)) / (e^x + e^(-x))

What it does:

• Large positive input → close to 1
• Large negative input → close to -1
• Around zero → around 0

Also S-shaped, but centered at zero.

Example:

Tanh(5) \u2248 0.99
Tanh(0) = 0
Tanh(-5) \u2248 -0.99

When to use it:

Sometimes in hidden layers when you need negative values.

Better than sigmoid for hidden layers because it's zero-centered. But ReLU is usually still better.

The problem:

Also has vanishing gradient (less severe than sigmoid).

Quick Comparison

Function	Range	Speed	Use Case	Main Issue
ReLU	0 to ∞	Very fast	Hidden layers (default)	Can "die"
Sigmoid	0 to 1	Slower	Output (binary)	Vanishing gradient
Tanh	-1 to 1	Slower	Hidden layers	Vanishing gradient

Practical Example

Building an image classifier: cat vs dog.

Your network:

Input (pixels)
\u2193
Hidden Layer 1 → ReLU
\u2193
Hidden Layer 2 → ReLU
\u2193
Hidden Layer 3 → ReLU
\u2193
Output Layer → Sigmoid

Why:

• Layers 1-3 use ReLU: Fast, efficient. Extracts features (edges, shapes, textures).
• Output uses Sigmoid: Gives probability (0 = dog, 1 = cat).

If output is 0.85, you're 85% confident it's a cat.

Key Takeaway

Without activation functions:

• All layers collapse into one linear equation
• Network can only draw straight lines
• Deep learning doesn't work

With activation functions:

• Each layer learns something new
• Network creates complex, curved decision boundaries
• Deep learning becomes possible

Think of it this way:

Linear functions = trying to draw a circle using only a ruler.

Non-linear activation functions = you can draw curves, circles, any shape needed.

Other Activation Functions

You'll hear about:

• Leaky ReLU
• ELU (Exponential Linear Unit)
• Swish
• GELU

These are variations trying to fix specific problems.

For learning, stick with ReLU, Sigmoid, and Tanh. They cover 90% of cases.

Once you understand the basics, explore the rest.

Next Week

Now you know why activation functions are critical and how the main ones work.

Next question: How does a neural network know if it's getting better or worse?

That's where loss functions come in.

Next week, we'll cover how neural networks measure their mistakes and why choosing the right loss function matters.