What Are Tensors? (And Why Modern AI Needs Them)

Hey folks,

Over the past seven weeks, we covered the fundamentals: how neural networks work, how they learn, and how training transforms random weights into working models.

This week: The data structure that makes modern AI possible.

Everything we've covered so far works with simple inputs, individual numbers or small lists. But real-world AI handles images, videos, and text sequences. For that, we need tensors.

Let's break it down.

The Problem with Simple Data Structures

The neural networks from Issues #34-40 worked with straightforward inputs:

Example: Predicting house prices

Input: [3 bedrooms, 2000 sq ft, 2 bathrooms]
Output: $450,000

Three numbers in, one number out. Simple.

But what about an image classifier?

A small 28×28 pixel grayscale image contains 784 numbers (one per pixel). A color photo at 224×224 pixels contains 150,528 numbers (224 × 224 × 3 RGB channels).

How do you organize 150,528 numbers efficiently? How do you process 32 images simultaneously in a batch?

You need a better data structure. That's where tensors come in.

What Tensors Actually Are

A tensor is a multi-dimensional array of numbers with a well-defined shape.

Think of tensors as containers that organize data by dimensions:

0D Tensor (Scalar): A single number

5

1D Tensor (Vector): A list of numbers

[1, 2, 3, 4, 5]

2D Tensor (Matrix): A grid of numbers

[[1, 2, 3],
 [4, 5, 6],
 [7, 8, 9]]

3D Tensor: A cube of numbers (think: a stack of matrices)

Multiple 2D grids stacked on top of each other

4D, 5D, 6D+ Tensors: Even higher dimensional structures

The key insight: Tensors aren't complex math, they're organized containers for data.

The Dimension Ladder

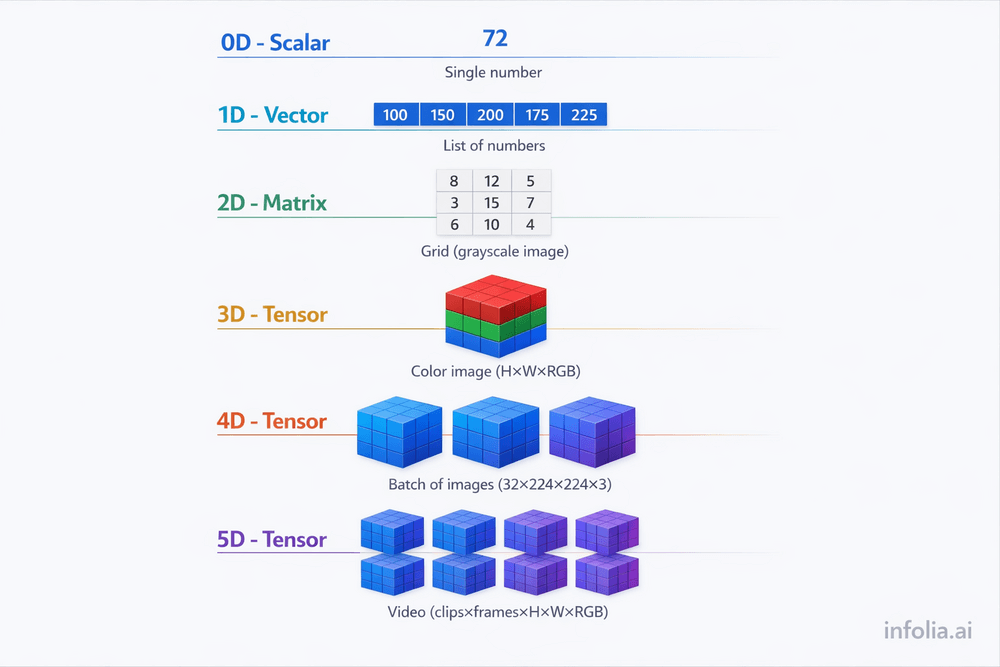
Let's climb from simple to complex:

Scalar (0D Tensor): Single number. temperature = 72
Shape: () | Use: Single predictions

Vector (1D Tensor): List of numbers. [100, 150, 200, 175]
Shape: (5,) | Use: Word embeddings, audio samples

Matrix (2D Tensor): Grid of numbers.
Shape: (28, 28) | Use: Grayscale images, spreadsheets

3D Tensor: Stack of matrices.
Shape: (224, 224, 3) | Use: Color images (height × width × RGB channels)

4D Tensor: Batch of 3D tensors.
Shape: (32, 224, 224, 3) | Use: 32 color images for training

5D+ Tensor: Even higher dimensions.
Shape: (10, 30, 224, 224, 3) | Use: Video (10 clips, 30 frames each)

Real-World Example: Understanding Image Tensors

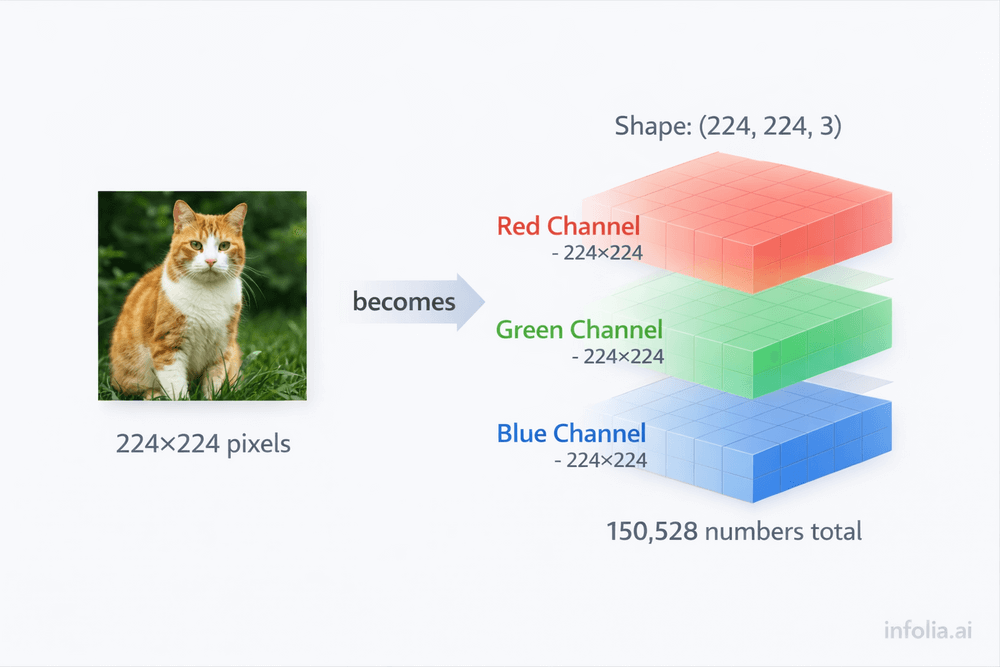
Let's break down how images become tensors:

Grayscale Image (2D Tensor)

A 28×28 pixel grayscale image from MNIST (handwritten digits):

Shape: (28, 28)
Total values: 784 numbers
Each value: 0-255 (pixel brightness)

This is just a 2D matrix. Each number represents one pixel's brightness.

Color Image (3D Tensor)

A 224×224 pixel color photo:

Shape: (224, 224, 3)
Total values: 150,528 numbers
Dimensions: height × width × channels

The third dimension (3) represents RGB:

• Channel 0: Red intensity at each pixel
• Channel 1: Green intensity at each pixel
• Channel 2: Blue intensity at each pixel

Think of it as three 224×224 grayscale images stacked together—one for red, one for green, one for blue.

Batch of Color Images (4D Tensor)

Training neural networks processes multiple images simultaneously:

Shape: (32, 224, 224, 3)
Total values: 4,816,896 numbers
Dimensions: batch_size × height × width × channels

This is 32 color images, each 224×224×3, organized into a single 4D tensor.

Why batch processing?

• Faster training (GPUs process batches efficiently)
• More stable gradient calculations
• Better memory utilization

Shape vs Rank: Avoiding Confusion

Two critical tensor concepts:

Shape: The size of each dimension

tensor.shape = (32, 224, 224, 3)

Tells you: 32 images, each 224×224 pixels, with 3 color channels.

Rank: The number of dimensions

tensor.rank = 4

Tells you: This is a 4D tensor (4 dimensions).

Common confusion:

• "3D tensor" doesn't mean 3D graphics
• It means a tensor with 3 dimensions (like a color image: height × width × channels)

Tensor Operations: What You Can Do

Tensors support mathematical operations optimized for GPUs:

Element-wise operations: Apply operations to each element. Adding tensors, multiplying by scalars. Used for normalizing pixel values, applying activation functions.

Matrix multiplication: Fundamental to neural networks. result = weights @ input. Every forward propagation step uses this.

Reshaping: Change shape without changing data. Flatten (28, 28) image to (784,) vector. Used when converting images for fully-connected layers.

Broadcasting: Automatically expand smaller tensors. Add scalar 10 to a matrix, and it applies to every element. Used for adding bias terms.

Why GPUs Love Tensors

Tensors enable parallel processing, which is why GPUs accelerate deep learning so dramatically.

CPU approach (sequential):

Process pixel 1
Process pixel 2
Process pixel 3
... (150,528 pixels later)
Done!

GPU approach (parallel):

Process all 150,528 pixels simultaneously
Done!

Tensors organize data so GPUs can apply the same operation to thousands of elements at once. A task that takes a CPU 10 minutes might take a GPU 10 seconds.

This is why modern AI requires GPUs: Not because GPUs are "faster," but because tensors enable massive parallelization.

Why Modern Architectures Need Tensors

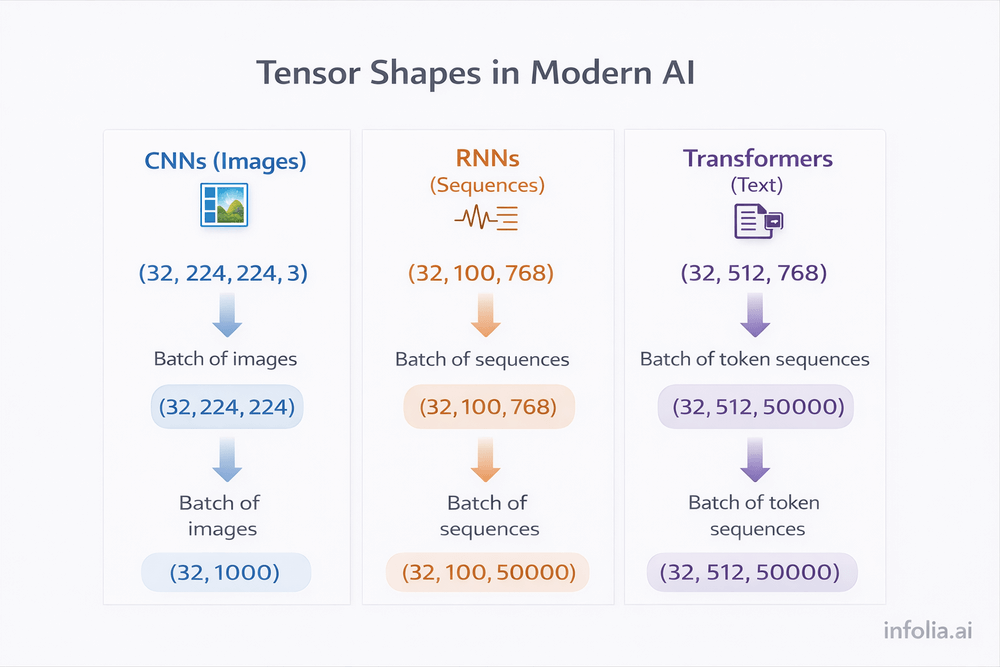
Every modern neural network architecture operates on tensors:

Convolutional Neural Networks (CNNs):

• Input: 4D tensor (batch, height, width, channels)
• Process images by sliding filters across spatial dimensions
• Output: 4D tensor with learned features

Recurrent Neural Networks (RNNs):

• Input: 3D tensor (batch, time_steps, features)
• Process sequences (text, audio, time series)
• Output: 3D tensor with temporal patterns

Transformers:

• Input: 3D tensor (batch, sequence_length, embedding_dimension)
• Process text using attention mechanisms
• Power models like ChatGPT, BERT, GPT-4

You can't understand these architectures without understanding tensors. They're the foundation everything else builds on.

Practical Example: Image Classification Pipeline

Let's trace how tensors flow through an image classifier:

Step 1: Load 32 color photos (224×224 pixels each)

Step 2: Convert to tensor → Shape: (32, 224, 224, 3) = 4.8M numbers

Step 3: Normalize pixel values from [0, 255] to [0, 1]

Step 4: Convolutional layers process spatial dimensions → extract features

Step 5: Output predictions → Shape: (32, 1000) = 32 images, 1000 possible classes each

The entire pipeline operates on tensors from start to finish.

Common Tensor Shapes You'll See

Image classification:

• Input: (batch, height, width, channels) → (32, 224, 224, 3)
• Output: (batch, num_classes) → (32, 1000)

Text processing:

• Input: (batch, sequence_length, embedding_dim) → (32, 512, 768)
• Output: (batch, sequence_length, vocab_size) → (32, 512, 50000)

Time series:

• Input: (batch, time_steps, features) → (32, 100, 10)
• Output: (batch, prediction_window) → (32, 24)

Recognizing these patterns helps you understand how different architectures work.

Key Takeaway

Tensors are organized containers for multi-dimensional data.

They're not complex math—they're practical data structures:

• 0D (scalar): A single number
• 1D (vector): A list
• 2D (matrix): A grid
• 3D+: Stacked grids

Why they matter:

• Real-world data is multi-dimensional (images, video, sequences)
• Tensors organize this data efficiently
• GPUs process tensors in parallel (massive speedup)
• Every modern architecture (CNNs, RNNs, Transformers) operates on tensors

The insight: Tensors aren't optional advanced math. They're the fundamental data structure of modern AI.

Master tensors, and CNNs, RNNs, and Transformers become much easier to understand.

What's Next

Next week: Convolutional Neural Networks (CNNs) and how they process image tensors.

Read the full AI Learning series → Learn AI